DINÁMICA: SEGUNDA LEY DE NEWTON

SEGUNDA LEY DE NEWTON

¿Qué es la segunda ley de Newton?

En el mundo de la física introductoria, la segunda ley de Newton es una de las leyes más importantes que aprenderás. Es utilizada en casi cada capítulo de cada libro de texto de física, así que es importante dominar esta ley tan pronto como sea posible.

Sabemos que los objetos solo pueden acelerar si hay fuerzas actuando sobre ellos. La segunda ley de Newton nos dice exactamente cuánto puede acelerar un objeto para una fuerza neta dada.

$\Large a=\dfrac{\Sigma F}{m}$a, equals, start fraction, \Sigma, F, divided by, m, end fraction

Para ser claros, $a$a es la aceleración del objeto, $\Sigma F$\Sigma, F es la fuerza neta sobre el objeto, y $m$m es la masa del objeto.

$F=ma$F, equals, m, a$\Sigma F$\Sigma, F$m$m$a$a

$a=\dfrac{\Sigma F}{m}$a, equals, start fraction, \Sigma, F, divided by, m, end fraction

$ma$m, a$ma$m, a$ma$m, a

Al observar la forma de la segunda ley de Newton que se muestra arriba, vemos que la aceleración es proporcional a la fuerza neta $\Sigma F$\Sigma, F, y es inversamente proporcional a la masa $m$m. En otras palabras, si la fuerza neta fuera duplicada, la aceleración del objeto sería el doble. Del mismo modo, si la masa del objeto fuera duplicada, su aceleración sería la mitad.

¿Qué significa la fuerza neta?

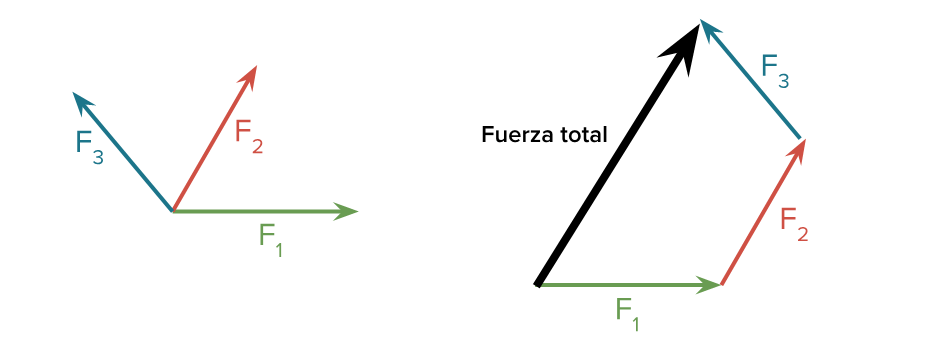
Una fuerza es un empujón o un jalón, y la fuerza neta $\Sigma F$\Sigma, F es la fuerza total —o suma de las fuerzas— ejercida sobre un objeto. Sumar vectores es un poco diferente que sumar números normales. Cuando sumamos vectores debemos tomar en cuenta su dirección. La fuerza neta es la suma vectorial de todas las fuerzas ejercidas sobre un objeto.

$30 \text{ N}$$20 \text{ N}$

Por ejemplo, considera las dos fuerzas de magnitud 30 N y 20 N que se ejercen hacia la derecha y hacia la izquierda sobre la oveja mostrada arriba, respectivamente. Si suponemos que la derecha es la dirección positiva, la fuerza neta sobre la oveja puede se puede encontrar con

$\Sigma F = 30\text{ N} - 20\text{ N}$\Sigma, F, equals, 30, start text, space, N, end text, minus, 20, start text, space, N, end text

$\Sigma F = 10\text{ N}$\Sigma, F, equals, 10, start text, space, N, end text hacia la derecha

Si hubiera más fuerzas horizontales, podríamos encontrar la fuerza neta al sumar todas las fuerzas a la derecha y al restar todas las fuerzas a la izquierda.

Como la fuerza es un vector, podemos escribir la segunda ley de Newton como $\vec a=\dfrac{\Sigma \vec F}{m}$a, with, vector, on top, equals, start fraction, \Sigma, F, with, vector, on top, divided by, m, end fraction. Esto muestra que la dirección del vector total de aceleración apunta en la misma dirección que el vector de fuerza neta. En otras palabras, si la fuerza neta $\Sigma F$\Sigma, F apunta a la derecha, la aceleración $a$a debe apuntar a la derecha.

¿Cómo utilizamos la segunda ley de Newton?

Si el problema que estás analizando tiene muchas fuerzas en muchas direcciones, a menudo es más fácil analizar cada dirección de manera independiente.

En otras palabras, para la dirección horizontal podemos escribir

$\Large a_x=\dfrac{\Sigma F_x}{m}$a, start subscript, x, end subscript, equals, start fraction, \Sigma, F, start subscript, x, end subscript, divided by, m, end fraction

Esto nos dice que la aceleración $a_x$a, start subscript, x, end subscript en la dirección horizontal es igual a la fuerza neta en la dirección horizontal, $\Sigma F_x$\Sigma, F, start subscript, x, end subscript, dividida entre la masa.

Del mismo modo, para la dirección vertical podemos escribir

$\Large a_y=\dfrac{\Sigma F_y}{m}$a, start subscript, y, end subscript, equals, start fraction, \Sigma, F, start subscript, y, end subscript, divided by, m, end fraction

Esto nos dice que la aceleración $a_y$a, start subscript, y, end subscript en la dirección vertical es igual a la fuerza neta en la dirección vertical, $\Sigma F_y$\Sigma, F, start subscript, y, end subscript, dividida entre la masa.

Cuando usemos estas ecuaciones debemos tener cuidado de solo sustituir fuerzas horizontales en la forma horizontal de la segunda ley de Newton, y de sustituir fuerzas verticales en la forma vertical de la segunda ley de Newton. Hacemos esto porque las fuerzas horizontales solo afectan la aceleración horizontal, y las fuerzas verticales solo afectan la aceleración vertical. Por ejemplo, considera una gallina de masa $m$m sobre la que se están ejerciendo fuerzas de magnitud $\redD{F_1}$start color #e84d39, F, start subscript, 1, end subscript, end color #e84d39, $\blueD{F_2}$start color #11accd, F, start subscript, 2, end subscript, end color #11accd, $\greenD {F_3}$start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54 y $F_4$F, start subscript, 4, end subscript en las direcciones que se muestran a continuación.

$F_4$$F_1$$F_2$$F_3$

Las fuerzas $\redD{F_1}$start color #e84d39, F, start subscript, 1, end subscript, end color #e84d39 y $\greenD {F_3}$start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54 afectan a la aceleración horizontal, ya que actúan a lo largo de la dirección horizontal. Al aplicar la segunda ley de Newton a la dirección horizontal, y suponiendo que la dirección hacia la derecha es positiva, obtenemos

$a_x=\dfrac{\Sigma F_x}{m}=\dfrac{\redD{F_1}-\greenD {F_3}}{m}$a, start subscript, x, end subscript, equals, start fraction, \Sigma, F, start subscript, x, end subscript, divided by, m, end fraction, equals, start fraction, start color #e84d39, F, start subscript, 1, end subscript, end color #e84d39, minus, start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54, divided by, m, end fraction

Del mismo modo, las fuerzas $\blueD{F_2}$start color #11accd, F, start subscript, 2, end subscript, end color #11accd y $F_4$F, start subscript, 4, end subscript afectan a la aceleración vertical, ya que actúan a lo largo de la dirección vertical. Al aplicar la segunda ley de Newton a la dirección vertical, y suponiendo que hacia arriba es la dirección positiva, obtenemos

$a_y=\dfrac{\Sigma F_y}{m}=\dfrac{\blueD{F_2}-F_4}{m}$a, start subscript, y, end subscript, equals, start fraction, \Sigma, F, start subscript, y, end subscript, divided by, m, end fraction, equals, start fraction, start color #11accd, F, start subscript, 2, end subscript, end color #11accd, minus, F, start subscript, 4, end subscript, divided by, m, end fraction

Advertencia: un error común que comete la gente es sustituir una fuerza vertical en una ecuación horizontal, y viceversa.

¿Qué hacemos cuando una fuerza está dirigida en un ángulo?

Cuando las fuerzas se dirigen en diagonales, todavía podemos analizar las fuerzas en cada dirección de manera independiente. Pero las fuerzas diagonales contribuirán a la aceleración tanto en la dirección vertical como en la horizontal.

Por ejemplo, digamos que la fuerza $\greenD {F_3}$start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54 sobre la gallina ahora se dirige en un ángulo $\theta$theta como se muestra a continuación.

$\theta$$F_4$$F_1$$F_2$$F_3$

La fuerza $\greenD {F_3}$start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54 afectará tanto a la aceleración vertical como a la horizontal, pero solo la componente horizontal de $\greenD {F_3}$start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54 afectará la aceleración horizontal y solo la componente vertical de $\greenD {F_3}$start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54 afectará a la aceleración vertical. Así que vamos a separar la fuerza $\greenD {F_3}$start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54 en sus componentes horizontal y vertical, como se muestra a continuación.

$\theta$$F_4$$F_1$$F_2$$F_3$$F_{3x}$$F_{3y}$

Ahora vemos que la fuerza $\greenD{F_3}$start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54 puede ser considerada como la composición de la fuerza horizontal $\greenD{F_{3x}}$start color #1fab54, F, start subscript, 3, x, end subscript, end color #1fab54 y la fuerza vertical $\greenD{F_{3y}}$start color #1fab54, F, start subscript, 3, y, end subscript, end color #1fab54.

Al usar trigonometría, podemos encontrar la magnitud de la componente horizontal con $\greenD {F_{3x}}=\greenD {F_{3}}\text{cos}\theta$start color #1fab54, F, start subscript, 3, x, end subscript, end color #1fab54, equals, start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54, start text, c, o, s, end text, theta. Del mismo modo, podemos encontrar la magnitud de la componente vertical con $\greenD {F_{3y}}=\greenD {F_{3}}\text{sin}\theta$start color #1fab54, F, start subscript, 3, y, end subscript, end color #1fab54, equals, start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54, start text, s, i, n, end text, theta.

$\text{sin}\theta=\dfrac{\text{cateto opuesto}}{\text{hipotenusa}}$start text, s, i, n, end text, theta, equals, start fraction, start text, c, a, t, e, t, o, space, o, p, u, e, s, t, o, end text, divided by, start text, h, i, p, o, t, e, n, u, s, a, end text, end fraction$\greenD{F_{3y}}$start color #1fab54, F, start subscript, 3, y, end subscript, end color #1fab54$\greenD{F_3}$start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54

$\text{sin}\theta=\dfrac{\greenD{F_{3y}}}{\greenD{F_3}}$start text, s, i, n, end text, theta, equals, start fraction, start color #1fab54, F, start subscript, 3, y, end subscript, end color #1fab54, divided by, start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54, end fraction

$\greenD{F_{3y}}$start color #1fab54, F, start subscript, 3, y, end subscript, end color #1fab54

$\greenD{F_{3y}}=\greenD{F_3}\text{sin}\theta$start color #1fab54, F, start subscript, 3, y, end subscript, end color #1fab54, equals, start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54, start text, s, i, n, end text, theta

---

$\text{cos}\theta=\dfrac{\text{cateto adyacente}}{\text{hipotenusa}}$start text, c, o, s, end text, theta, equals, start fraction, start text, c, a, t, e, t, o, space, a, d, y, a, c, e, n, t, e, end text, divided by, start text, h, i, p, o, t, e, n, u, s, a, end text, end fraction$\greenD{F_{3x}}$start color #1fab54, F, start subscript, 3, x, end subscript, end color #1fab54$\greenD{F_3}$start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54

$\text{cos}\theta=\dfrac{\greenD{F_{3x}}}{\greenD{F_3}}$start text, c, o, s, end text, theta, equals, start fraction, start color #1fab54, F, start subscript, 3, x, end subscript, end color #1fab54, divided by, start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54, end fraction

$\greenD{F_{3x}}$start color #1fab54, F, start subscript, 3, x, end subscript, end color #1fab54

$\greenD{F_{3x}}=\greenD{F_3}\text{cos}\theta$start color #1fab54, F, start subscript, 3, x, end subscript, end color #1fab54, equals, start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54, start text, c, o, s, end text, theta

Ahora podemos proceder como siempre sustituyendo todas las fuerzas dirigidas horizontalmente en la forma horizontal de la segunda ley de Newton.

$a_x=\dfrac{\Sigma F_x}{m}=\dfrac{\redD{F_1}-\greenD {F_{3x}}}{m}=\dfrac{\redD{F_1}-\greenD {F_{3}}\text{cos}\theta}{m}$a, start subscript, x, end subscript, equals, start fraction, \Sigma, F, start subscript, x, end subscript, divided by, m, end fraction, equals, start fraction, start color #e84d39, F, start subscript, 1, end subscript, end color #e84d39, minus, start color #1fab54, F, start subscript, 3, x, end subscript, end color #1fab54, divided by, m, end fraction, equals, start fraction, start color #e84d39, F, start subscript, 1, end subscript, end color #e84d39, minus, start color #1fab54, F, start subscript, 3, end subscript, end color #1fab54, start text, c, o, s, end text, theta, divided by, m, end fraction

Del mismo modo, podemos sustituir todas la fuerzas dirigidas verticalmente en la forma vertical de la segunda ley de Newton.

$a_y=\dfrac{\Sigma F_y}{m}=\dfrac{\blueD{F_2}-F_4+\greenD{F_{3y}}}{m}=\dfrac{\blueD{F_2}-F_4+\greenD{F_{3}}\text{sin}\theta}{m}$