DINÁMICA DEL MOVIMIENTO CIRCULAR FUNDAMENTOS

Estimados alumnos vamos a repasar un nuevo tema, revisen la teoría del libro de texto, repasen los vídeos que se adjuntan y realicen los ejercicios del mismo libro, que se proponen mas adelante.

Si no entienden un tema vuelvan a repasar los vídeos y cualquier inquietud lo ponen en el foro para responderlas.

¿Qué es la aceleración centrípeta?

¿Un objeto puede acelerar si se está moviendo con rapidez contante? ¡Sí! Al principio, a mucha gente esto les parece contraintuitivo porque se les olvida que los cambios en la dirección del movimiento de un objeto, incluso si el objeto mantiene una rapidez constante, siguen contando como aceleración.

La aceleración es un cambio en la velocidad, ya sea en su magnitud —es decir, en su rapidez— o en su dirección, o en ambas. En el movimiento circular uniforme, la dirección de la velocidad cambia constantemente, así que siempre hay una aceleración asociada, aunque es posible que la rapidez sea constante. Tú puedes experimentar esta aceleración al dar una vuelta en una esquina en el automóvil: si mantienes estable el volante durante la vuelta y vas con una rapidez constante, te estás moviendo en movimiento circular uniforme. Lo que observas es una aceleración hacia los lados porque tú y el automóvil están cambiando de dirección. Mientras más cerrada sea la curva y mayor sea tu rapidez, más perceptible será esta aceleración. En esta sección vamos a examinar la dirección y la magnitud de esa aceleración.

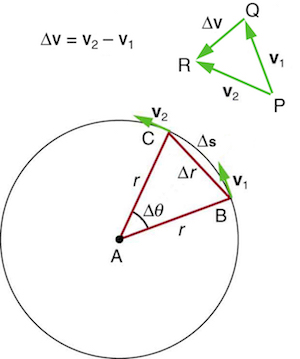
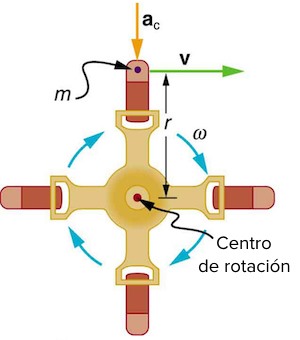
La siguiente figura muestra un objeto que se mueve en una trayectoria circular con una rapidez constante. La dirección de la velocidad instantánea se muestra en dos puntos a lo largo de la trayectoria. La dirección de la aceleración es hacia el centro de rotación, el centro de la trayectoria circular. Esta dirección se muestra en la figura con el diagrama de vectores. A la aceleración de un objeto que se mueve en movimiento circular uniforme, como resultado de una fuerza neta externa, la llamamos aceleración centrípeta 

${}^c$a, start subscript, c, end subscript

Centrípeta significa “hacia el centro” o “que busca el centro”.

Se muestran las direcciones de la velocidad de un objeto en dos puntos diferentes, $\text B$start text, B, end text y $\text C$start text, C, end text, y se observa que el cambio en velocidad, $\Delta v$delta, v, apunta aproximadamente hacia el centro de curvatura. Para ver lo que sucede instantáneamente, los puntos $\text B$start text, B, end text y $\text C$start text, C, end text deben estar muy cerca y $\Delta \theta$delta, theta debe ser muy pequeño. Luego encontraremos que $\Delta v$delta, v apunta directamente hacia el centro de curvatura.

Puesto que $a_c=\dfrac{\Delta v}{\Delta t}$a, start subscript, c, end subscript, equals, start fraction, delta, v, divided by, delta, t, end fraction, la aceleración también es hacia el centro. Debido a que $\Delta \theta$delta, theta es muy pequeño, la longitud del arco $\Delta s$delta, s es igual a la longitud de la cuerda $\Delta r$delta, r para pequeñas diferencias de tiempo. Crédito de la imagen: Openstax College Physics

La dirección de la aceleración centrípeta es hacia el centro del círculo, pero ¿cuál es su magnitud? Observa que el triángulo formado por los vectores de velocidad y el triángulo formado por los radios $r$r y $\Delta s$delta, s son semejantes. Los dos triángulos $ABC$A, B, C y $PQR$P, Q, R son triángulos isósceles con dos lados iguales. Los dos lados iguales del triángulo del vector de velocidad son la rapidez $v_1=v_2=v$v, start subscript, 1, end subscript, equals, v, start subscript, 2, end subscript, equals, v. Al usar las propiedades de dos triángulos semejantes, obtenemos que $\dfrac{\Delta v}{v}=\dfrac{\Delta s}{r}$start fraction, delta, v, divided by, v, end fraction, equals, start fraction, delta, s, divided by, r, end fraction.

La aceleración es $\dfrac{\Delta v}{\Delta t}$start fraction, delta, v, divided by, delta, t, end fraction, así que primero despejamos $\Delta v$delta, v de la expresión anterior:

$\Delta v=\dfrac{v}{r}\Delta s$delta, v, equals, start fraction, v, divided by, r, end fraction, delta, s

Si dividimos ambos lados entre $\Delta t$delta, t obtenemos lo siguiente:

$\dfrac{\Delta v}{\Delta t}=\dfrac{v}{r}\times \dfrac{\Delta s}{\Delta t}$start fraction, delta, v, divided by, delta, t, end fraction, equals, start fraction, v, divided by, r, end fraction, times, start fraction, delta, s, divided by, delta, t, end fraction

Por último, al observar que $\dfrac{\Delta v}{\Delta t}=a_c$start fraction, delta, v, divided by, delta, t, end fraction, equals, a, start subscript, c, end subscript y que $\dfrac{\Delta s}{\Delta t}=v$start fraction, delta, s, divided by, delta, t, end fraction, equals, v, la rapidez lineal o tangencial, vemos que la magnitud de la aceleración centrípeta es $a_c=\dfrac{v^2}{r}$a, start subscript, c, end subscript, equals, start fraction, v, squared, divided by, r, end fraction.

Esta es la aceleración de un objeto en un círculo de radio $r$r con una rapidez $v$v. Entonces, la aceleración centrípeta es mayor cuando la rapidez es mayor y en curvas más cerradas, o radios más pequeños, como te habrás dado cuenta al conducir un automóvil. Pero es algo sorprendente que $a_c$a, start subscript, c, end subscript sea proporcional al cuadrado de la rapidez, lo que implica que, por ejemplo, es cuatro veces más difícil tomar una curva a 100 km/h que a 50 km/h. Una esquina cerrada tiene un radio pequeño, así que $a_c$a, start subscript, c, end subscript es mayor para vueltas más cerradas, como probablemente te habrás dado cuenta.

¿Qué es una centrífuga?

Una centrífuga es un dispositivo rotatorio que se usa para separar muestras de diferentes densidades. Una aceleración centrípeta alta reduce significativamente el tiempo necesario para que ocurra la separación y hace que esta sea posible con muestras pequeñas. Las centrífugas se usan en una variedad de aplicaciones en la ciencia y en la medicina, incluyendo la separación de suspensiones de una sola célula como bacterias, virus y células de sangre de un medio líquido, y la separación de macromoléculas —tales como ADN y proteínas— de una solución.

Una partícula de masa $m$m en una centrífuga está rotando con rapidez constante. Debe acelerarse de manera perpendicular a su velocidad o continuaría moviéndose en línea recta. Crédito de la imagen: Openstax College Physics

A menudo, las centrífugas se clasifican en términos de su aceleración centrípeta con respecto a la aceleración debida a la gravedad, $g$g. Una aceleración centrípeta máxima de cientos de miles de veces la de $g$g es posible en un vacío. Las centrífugas humanas, centrífugas extremadamente grandes, se han usado para probar la tolerancia que tienen los astronautas a los efectos de aceleraciones mayores que la de la gravedad de la Tierra.

¿Qué es la inercia rotacional?

La inercia rotacional es una propiedad de cualquier objeto que puede girar. Es un valor escalar que nos indica qué tan difícil es cambiar la velocidad de rotación del objeto alrededor de un eje de rotación determinado.

En mecánica rotacional, la inercia rotacional desempeña un papel similar al de la masa en la mecánica lineal. De hecho, la inercia rotacional de un objeto depende de su masa. También depende de la distribución de esa masa respecto al eje de rotación.

Cuando una masa se aleja del eje de rotación se hace cada vez más más difícil cambiar la velocidad de rotación del sistema. Intuitivamente, esto es porque la masa lleva consigo más momento alrededor del círculo (debido a la velocidad más alta) y porque el vector de momento cambia más rápidamente. Estos dos efectos dependen de la distancia desde el eje.

La inercia rotacional se denota con el símbolo $I$I. Para un solo cuerpo como el de una pelota de tenis de masa $m$m que gira en un radio $r$r desde el eje de rotación (ver la Figura 1), la inercia rotacional es

$I = mr^2$I, equals, m, r, squared

y, en consecuencia, la inercia rotacional en el SI tiene unidades de $\mathrm{kg\cdot m ^ 2}$k, g, dot, m, squared.

A la inercia rotacional comúnmente se le conoce como el momento de inercia. También a veces se le llama el segundo momento de la masa; aquí 'segundo' se refiere al hecho de que depende de la longitud del brazo del momento al cuadrado.

Figura 1: una pelota de tenis atada que gira alrededor de un punto central

¿Cómo se relaciona la inercia rotacional con la segunda ley de Newton?

La inercia rotacional toma el lugar de la masa en la versión rotacional de la segunda ley de Newton.

Considera una masa $m$m unida a un extremo de una barra sin masa. El otro extremo de la barra está articulado para que el sistema pueda girar alrededor de la bisagra central como se muestra en la figura 2.

Figura 2: una masa que rota debido a una fuerza tangencial

Ahora comenzamos a rotar el sistema al aplicar una fuerza tangencial $F_T$F, start subscript, T, end subscript a la masa. De la segunda ley de Newton,

$F_T = m a_T$F, start subscript, T, end subscript, equals, m, a, start subscript, T, end subscript.

Esto también se puede escribir como

$F_T = m (r \alpha)$F, start subscript, T, end subscript, equals, m, left parenthesis, r, alpha, right parenthesis.

La segunda ley de Newton relaciona la fuerza con la aceleración. En la mecánica rotacional $\tau$tau toma el lugar de la fuerza. Al multiplicar ambos lados por el radio obtenemos la expresión deseada.

$\begin{aligned} F_T r &= m (r \alpha) r\\ \tau &= m r^2 \alpha \\ \tau &= I \alpha\end{aligned}$

Ahora esta expresión puede utilizarse para encontrar el comportamiento de una masa en respuesta a una torca conocida.