FUNDAMENTOS SOBRE GRAVITACIÓN (LAS LEYES DE KEPLER)

En esta semana vamos a repasar los conceptos fundamentales, acerca de la gravitación universal, en forma general:

 

Como tarea realizar los mapas conceptuales de este tema que consta en el libro de texto.

Primera ley

Una teoría imperfecta

Cuando los primeros astrónomos comenzaron a realizar un modelo del Sistema Solar, fue conveniente suponer que los planetas orbitaban alrededor del Sol en trayectorias perfectamente circulares. Es una idea que se remonta a Platón y que siguió siendo común hasta el siglo XVII.

El modelo heliocéntrico impreso en el libro “Sobre el movimiento de las esferas celestes” de Nicolás Copérnico, que se imprimió por primera vez en 1543

En el modelo heliocéntrico se supone que la Tierra gira alrededor del Sol en un círculo perfecto. Sin embargo, hay un problema con este modelo cuando observas atentamente el movimiento de los planetas. Aquí hay una secuencia de imágenes del Sol (tomadas desde la Tierra) en el transcurso de un año. Presta mucha atención al tamaño:

Crédito de la imagen: Observatorio solar Big Bear

¿Observas que el tamaño del Sol está cambiando regularmente? Esto no es el resultado de que el Sol esté creciendo y encogiéndose. Se trata del cambio de la distancia entre la Tierra y el Sol.

Órbitas elípticas

Johannes Kepler (1571 – 1630) fue un astrónomo alemán que se dio cuenta de que las órbitas circulares no funcionan mientras investigaba el movimiento orbital de Marte con detalle. Kepler le escribió acerca de su descubrimiento a un amigo astrónomo (David Fabricius) el 11 de octubre de 1605:

“Entonces, Fabricius, ya tengo esto: la trayectoria más coherente del planeta [Marte] es una elipse, a le que Durero también le llama óvalo, o ciertamente tan cerca de una elipse que la diferencia es insensible”.

Una elipse puede tener valores diferentes para su anchura y altura. Esto significa que el radio cambiará dependiendo del ángulo a través de toda la órbita. Una manera simple de pensar en una elipse es como la suma de dos círculos de tamaños diferentes que definen las coordenadas x y y respectivamente. En el siguiente ejemplo la coordenada x proviene del círculo más grande y la coordenada y proviene del círculo más pequeño. Convéncete a ti mismo de esto:

Crédito de la imagen: Peter Collingridge

Es importante observar que un círculo es un conjunto de puntos que está a una distancia fija del centro. Sin embargo una elipse es un conjunto de puntos que se encuentran a una cierta distancia de dos puntos específicos (llamados focos). Estos son dos puntos en el eje mayor tales que la suma de las distancias entre cualquier punto sobre la elipse y ambos focos es constante.

A continuación hay una ilustración interactiva. Puedes hacer clic y arrastrar los focos para cambiar la forma. Observa que las líneas verde y azul siempre suman la misma distancia:

Lo que conduce a la primera ley de Kepler:

La órbita de cada planeta es una elipse con el Sol en uno de los dos focos.

Preparación para la animación

Para dibujar una órbita elíptica definimos el radio del eje x (a) y el radio del eje y (b). El eje mayor es el más grande de los dos, el eje menor, el más pequeño. Tenga en cuenta que si a = b, entonces las ecuaciones son las mismas que las que usamos para un círculo perfecto.

x = a x cos(θ)

y = b x sin(θ)

Ahora podemos definir una elipse con tres propiedades: su centro, su eje principal y su eje menor.

Johannes Kepler fue más allá del descubrimiento de las órbitas elípticas, que describe en su primera ley.

Segunda ley

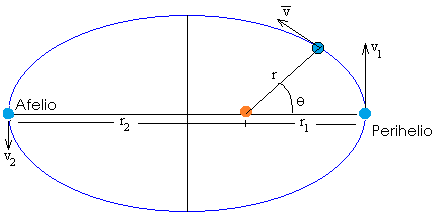
Velocidad de los planetas y sus órbitas

Kepler observó que los planetas no se mueven con una velocidad uniforme, sino que estos lo hacen con mayor rapidez mientras están más cerca al sol, y lo hacen con mayor lentitud, mientras más se alejan.

En ese momento, Kepler no sabía por qué los planetas y satélites se movían de la manera que había observado. Ahora podemos decir que esto ocurre gracias a que los cuerpos están bajo la influencia de un campo gravitacional.

Los cuerpos aceleran a medida que se acercan al campo y desaceleran a medida que se alejan de él, tal como un objeto desacelera cuando lo lanzas hacia arriba, pues está yendo en sentido contrario a la gravedad, y acelera al regresar a tu mano, cuando se mueve en la misma dirección de la gravedad.

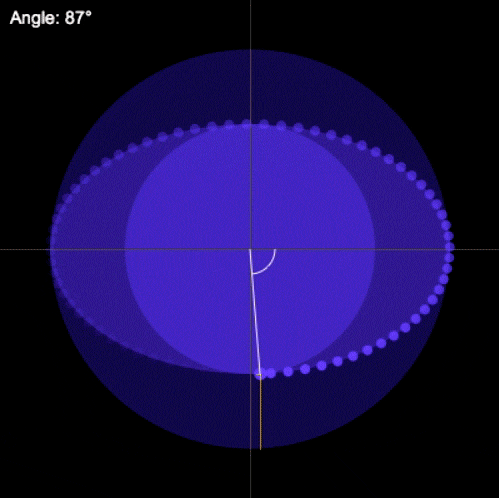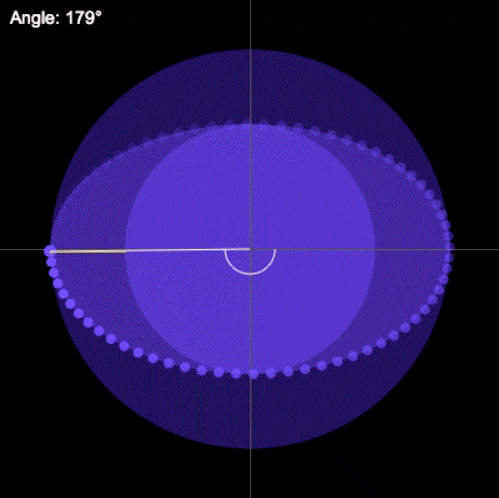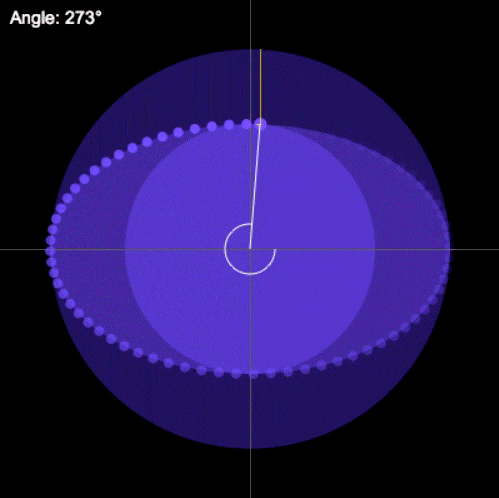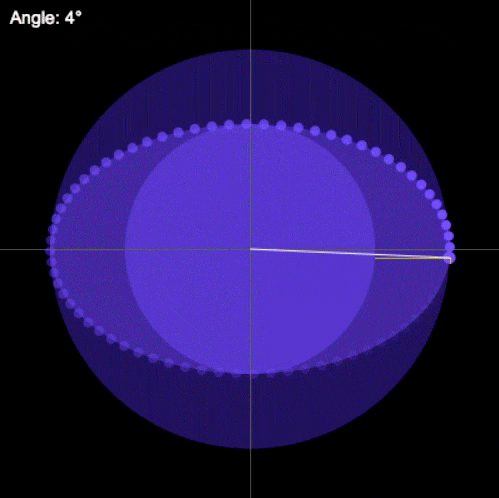
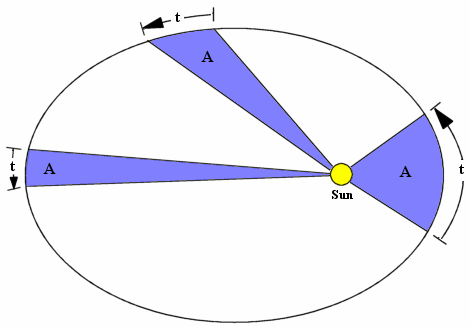
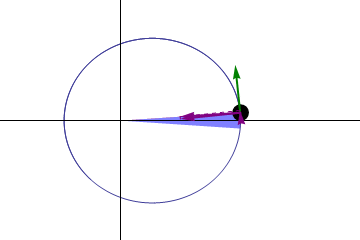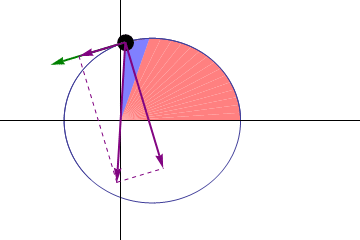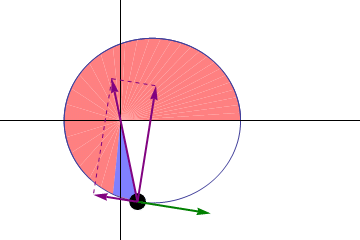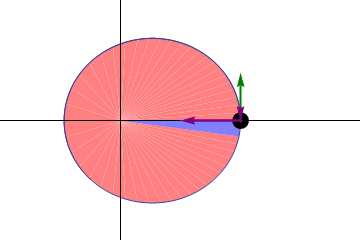
Sin embargo, a pesar de no contar con este marco teórico, Kepler pudo establecer una relación, gracias a su aguda observación y a sus conocimientos matemáticos. Descubrió que el área que barre el cuerpo en cualquier sección de la órbita, será la misma en un intervalo de tiempo igual, es decir:

La línea recta que une a cualquier planeta con el Sol, barre áreas iguales de espacio en intervalos iguales de tiempo.

Esta relación se expresa gráficamente de la siguiente manera:

Representación gráfica de la segunda ley de Kepler

Se barren áreas iguales en intervalos iguales de tiempo. Créditos: CC BY-SA 2.0.

Esta ley de las áreas es equivalente a la constancia del momento angular, esto quiere decir que cuando el planeta está más alejado del Sol su velocidad es menor que cuando está más cercano al Sol.

Animación de la segunda ley de Kepler.

Animación de la segunda ley de Kepler. Nota las diferentes velocidades con respecto a la distancia del foco. Créditos: Gonfer (talk) - Gonfer, CC BY-SA 3.0.

En el afelio y en el perihelio, al estar los planetas alineados en línea recta con su estrella, son los dos únicos puntos de la órbita en los que el radio vector y la velocidad son perpendiculares. En estos puntos, el momento angular $L$L es el producto de la masa del planeta, por su velocidad y por su distancia al centro del Sol:

$\Large L=mr_1\times v_1=mr_2\times v_2$L, equals, m, r, start subscript, 1, end subscript, times, v, start subscript, 1, end subscript, equals, m, r, start subscript, 2, end subscript, times, v, start subscript, 2, end subscript

Representación de la segunda ley de Kepler en perihelio y afelio.

Esta es la Segunda ley de Kepler.

Tercera ley

Períodos y radios orbitales: la Tercera ley de Kepler

Kepler, como todo científico, buscaba modelos matemáticos que pudieran explicar y predecir el comportamiento de su objeto de estudio. Luego de diez años del planteamiento de la segunda ley, encontró que el período de un planeta y su órbita estaban relacionados de la siguiente manera:

Los cuadrados de los 

periodos orbitales

 de los planetas son proporcionales a los cubos de su 

distancia promedio

 al Sol, es decir:

$\Large \dfrac{T^2}{R^3}=K$start fraction, T, squared, divided by, R, cubed, end fraction, equals, K

Esto quiere decir que para dos planetas (planeta 1 y planeta 2) orbitando una estrella, tenemos:

$\Large \dfrac{T_1^2}{R_1^3} = \dfrac{T_2^2}{R_2^3}$start fraction, T, start subscript, 1, end subscript, squared, divided by, R, start subscript, 1, end subscript, cubed, end fraction, equals, start fraction, T, start subscript, 2, end subscript, squared, divided by, R, start subscript, 2, end subscript, cubed, end fraction

Esta misma ecuación puede expresarse de la siguiente manera:

$\Large \dfrac{T_1^2}{T_2^2} = \dfrac{R_1^3}{R_2^3}$start fraction, T, start subscript, 1, end subscript, squared, divided by, T, start subscript, 2, end subscript, squared, end fraction, equals, start fraction, R, start subscript, 1, end subscript, cubed, divided by, R, start subscript, 2, end subscript, cubed, end fraction

Las leyes de Kepler se aplican no solo a los planetas, sino a todo satélite que orbite alrededor de cualquier cuerpo celeste.

Aplicaciones

Las leyes de Kepler nos ayudan a predecir el comportamiento de cuerpos celestes que orbitan otros cuerpos mayores.

Por ejemplo, la Luna orbita la Tierra con un periodo de 27.3 días, y su distancia promedio es de $3.84 \times 10^8\text { m}$3, point, 84, times, 10, start superscript, 8, end superscript, start text, space, m, end text hasta el centro de la Tierra. Si el radio de la Tierra es $6380\text{ km}$6380, start text, space, k, m, end text, ¿Podemos calcular el período de un satélite artificial que orbita a una altitud promedio de $1,500\text{ m}$1, comma, 500, start text, space, m, end text por encima de la superficie de nuestro planea?

¡La respuesta es sí!

Tenemos como datos:

$R_l$R, start subscript, l, end subscript=$3.84 \times 10^8\text { m}=3.84 \times 10^5\text { km}$3, point, 84, times, 10, start superscript, 8, end superscript, start text, space, m, end text, equals, 3, point, 84, times, 10, start superscript, 5, end superscript, start text, space, k, m, end text
$T_l$T, start subscript, l, end subscript= $27.3\text{ d}=655.2 \text{ h}$27, point, 3, start text, space, d, end text, equals, 655, point, 2, start text, space, h, end text
$R_s$R, start subscript, s, end subscript= $1500+6380=880\text{ km}$1500, plus, 6380, equals, 880, start text, space, k, m, end text

Y nos están pidiendo $T_s$T, start subscript, s, end subscript.

Según la tercera ley de Kepler, se cumple que:

$\dfrac{T_l^2}{T_s^2} = \dfrac{R_l^3}{R_s^3}$start fraction, T, start subscript, l, end subscript, squared, divided by, T, start subscript, s, end subscript, squared, end fraction, equals, start fraction, R, start subscript, l, end subscript, cubed, divided by, R, start subscript, s, end subscript, cubed, end fraction

Reemplazando:

$\begin{aligned} \dfrac{(655.2)^2}{T_s^2}&= \dfrac{(3.84 \times 10^5)^3}{(7880)^3}\\\\ T_s^2&=(655.2)^2\dfrac{(7880)^3}{(3.84 \times 10^5)^3}\\\\ T_s&=(655.2)\sqrt{\dfrac{(7880)^3}{(3.84 \times 10^5)^3}}\\\\ T_s &= 1.93\text{ h}\end{aligned}$

El satélite tendrá un periodo de 1.93 horas a una altura de $1500\text{ km}$1500, start text, space, k, m, end text sobre la superficie terrestre. ¡Increíble!